Vapnik–Chervonenkis Dimension and Polynomial Classifiers
In this post we will explore a rather unusual sort of binary classifier: the generalized polynomial classifiers. Our primary goal is to determine analytical bounds on the VC-dimension of this family of classifiers, giving some indication as to their potential expressive power.
Generalized Polynomial Classifiers
A generalized polynomial classifier is a binary classifier of the form
![Rendered by QuickLaTeX.com \[H(x) = \begin{cases}+1 &\text{if } p(x) > 0 \\-1 &\text{if } p(x) \le 0\end{cases}\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-4af024ef4deb37735971f678e2e66a53_l3.png)
for multi-variate polynomials
Depending on the dimension of the feature space and the value of ![]() , these classifiers resemble some more familiar models:
, these classifiers resemble some more familiar models:
- When our feature space is
 and
and  is arbitrary, the polynomial
is arbitrary, the polynomial 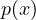 is a conventional polynomial of a single real variable:
is a conventional polynomial of a single real variable:
In this case, finding![Rendered by QuickLaTeX.com \[p(x) = a_0 + a_1x + \cdots a_{d}x^d\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-1537d661089a8c17fba6b7e41fcdf34b_l3.png)
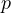 is a polynomial interpolation task, and
is a polynomial interpolation task, and 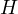 partitions the real line into positive and negative regions delineated by the roots of
partitions the real line into positive and negative regions delineated by the roots of 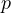 .
. - When our feature space is
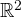 and
and 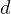 is arbitrary, the polynomial
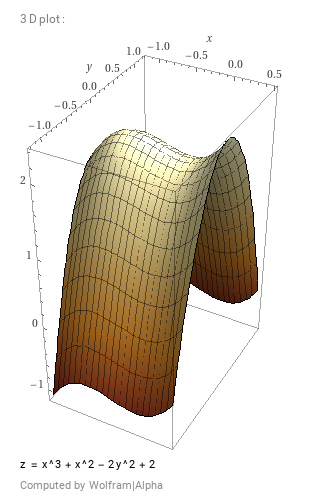
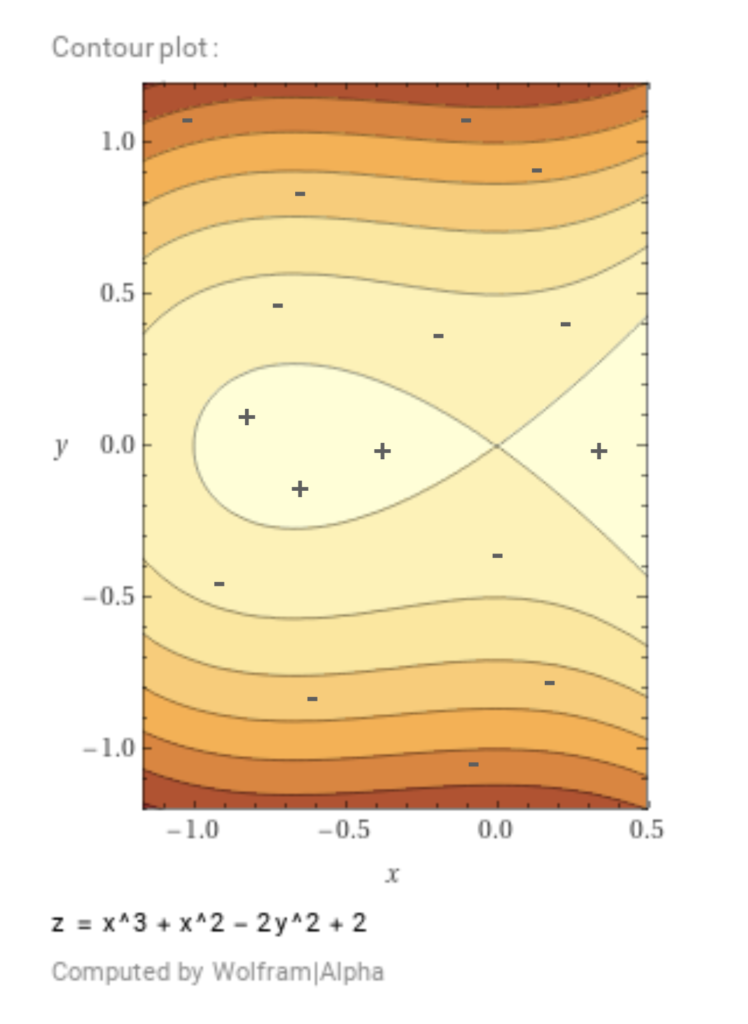
is arbitrary, the polynomial 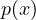 is a polynomial of two variables:
is a polynomial of two variables:
In this case, finding![Rendered by QuickLaTeX.com \[p(x, y) = a_0 + a_1x + a_2y + a_3x^2 + a_4y^2 + a_5xy + a_6x^3 + a_7x^2y + \cdots\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-124683c064dd0d1533052dcbb39aef4a_l3.png)
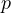 is a surface-fitting task, and the resulting
is a surface-fitting task, and the resulting 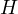 partitions the plane into regions delineated by the iso-contours
partitions the plane into regions delineated by the iso-contours 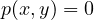 .
. - When our feature space is
 and
and  , we have a not-uncommon quadratic form:
, we have a not-uncommon quadratic form:
expressed in terms of conventional matrix-vector products.![Rendered by QuickLaTeX.com \[p(x) = A_0 + A_1x + x^\T A_2 x\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-d30fc7f4b4b607dbcce1f91cff6d9ead_l3.png)
- When our feature space is
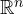 and
and 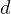 is arbitrary, we have the most general form
is arbitrary, we have the most general form
where![Rendered by QuickLaTeX.com \[p(x) = A_0 + A_1x + A_2x^2 + \cdots + A_dx^d\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-eeb6a0583750be75b2fff3d76582e4ab_l3.png)
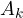 is a tensor1 of rank
is a tensor1 of rank 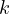 and
and 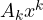 denotes the
denotes the 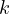 -mode product:
-mode product:
Hence,![Rendered by QuickLaTeX.com \[A_kx^k = \sum_{i_1, \cdots, i_k} A_k[i_1, \cdots, i_k]x[i_1] \cdots x[i_k]\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-4ca59f62af9df1d926b73c127417e42c_l3.png)
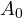 is a scalar,
is a scalar, 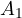 a vector,
a vector, 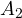 a matrix, etc.
a matrix, etc.
For example, over ![]() with
with ![]() , we have the general form:
, we have the general form:
![Rendered by QuickLaTeX.com \[p(x) = A_0 + \begin{pmatrix}A_1[0] \\ A_1[1] \\ A_1[2]\end{pmatrix}\begin{pmatrix}x \\ y \\ z\end{pmatrix} + \begin{pmatrix} A_2[0, 0] & A_2[0, 1] & A_2[0, 2] \\ A_2[1, 0] & A_2[1, 1] & A_2[1, 2] \\ A_2[2, 0] & A_2[2, 1] & A_2[2, 2] \\ \end{pmatrix}\begin{pmatrix}x \\ y \\ z\end{pmatrix}\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-9e17867f2a60ff43eb97ec1e68937d5b_l3.png)
A GPC can be viewed as a generalization of an SVM with a polynomial kernel. The number of coefficients (and hence the number of potentially trainable parameters) is given by:
![Rendered by QuickLaTeX.com \[\sum_{k=0}^d \binom{n+k-1}{k} = \binom{d+n}{d} = O\left(n^d\right)\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-54832c71a07bd390b869aadcc97e8748_l3.png)
Note that our chosen representation has some constant redundancy factor, which we can eliminate by stipulating WLOG that ![]() be upper-triangular. This exponential growth in the number of parameters indicates that the expressive power of a GPC is likely quite high. However, it also indicates that training may be impractical, and that overfitting may be a serious issue.
be upper-triangular. This exponential growth in the number of parameters indicates that the expressive power of a GPC is likely quite high. However, it also indicates that training may be impractical, and that overfitting may be a serious issue.
We will use the notation ![]() to denote the family of polynomial classifiers over
to denote the family of polynomial classifiers over ![]() of dimension
of dimension ![]() .
.
Note that since we are using a regression tool for classification, we need to develop a continuous encoding for discrete labels. We use the obvious choice:
![]()
![]()
VC Dimension
VC-dimension, short for Vapnik–Chervonenkis Dimension, is a measure of the expressive power of a family of classifiers. It is defined as the size of the largest set of points that can be correctly classified (by a member of the family in question) for any assignment of binary labels. We sometimes say that the point set is “shattered” by the classifier in this case.
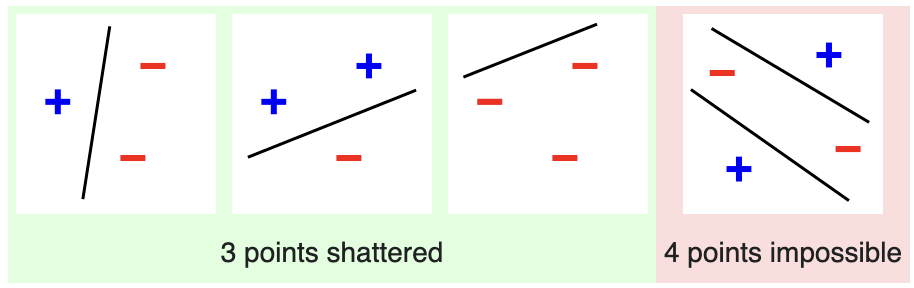
For example, consider a 2-dimensional feature space and the family of linear classifiers (i.e. classifiers whose decision boundaries are lines). This conventional family of classifiers is effectively just ![]() . Clearly, for any set of three points and any assignment of +/- labels, the data is linearly separable. However, no arrangements of four points can be shattered. There are two cases to consider:
. Clearly, for any set of three points and any assignment of +/- labels, the data is linearly separable. However, no arrangements of four points can be shattered. There are two cases to consider:
- All four points are contained in the convex hull. Assign labels such that only opposite points have the same label (as in Figure 1). The resulting arrangement is not linearly-separable.
- Only three points are contained in the convex hull. In this case, one point is necessarily contained in a triangle formed by the other three. Assign the three hull points + and the one internal point -. The resulting arrangement is not linearly-separable.
This argument shows that the VC dimension of the family of 2D linear classifiers is ![]() .
.
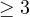 and
and 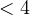 (case (2) omitted). (Image Credit)
(case (2) omitted). (Image Credit)As another point of reference, the VC-dimension of a neural network using the sigmoid non-linearity is known to be quadratic in the number of trainable parameters. Specifically, the VC-dimension is ![]() where
where ![]() and
and ![]() represent the edges and vertices in the network’s computation graph.
represent the edges and vertices in the network’s computation graph.
We will use the notation ![]() to denote the VC-dimension of a family of classifiers.
to denote the VC-dimension of a family of classifiers.
Theoretical Analysis of GPCs
First, an easy result on the monotonicty of the VC-dimension.
Theorem 1. Let ![]() and
and ![]() . Then,
. Then, ![]()
Proof. The result follows immediately from the fact that ![]() .
.
In the special case of polynomial classifiers over ![]() , the VC dimension is relatively straightforward to compute.
, the VC dimension is relatively straightforward to compute.
Theorem 2. ![]()
Proof. Since a polynomial of degree ![]() can have at most
can have at most ![]() roots, it can only partition the real line into at most
roots, it can only partition the real line into at most ![]() regions of alternating sign. Consequently, a set of
regions of alternating sign. Consequently, a set of ![]() sorted points with alternating labels:
sorted points with alternating labels:
![]()
cannot be correctly classified by any member of ![]() . Thus,
. Thus, ![]() .
.
Theorem 3. ![]()
Proof. For any set of ![]() points, there exists a polynomial (in fact, exactly one polynomial) of degree
points, there exists a polynomial (in fact, exactly one polynomial) of degree ![]() that interpolates the points. Thus, any given labelled points
that interpolates the points. Thus, any given labelled points ![]() can be classified exactly regardless of labelling by constructing the interpolating polynomial (by lagrange interpolation, for example). Thus,
can be classified exactly regardless of labelling by constructing the interpolating polynomial (by lagrange interpolation, for example). Thus, ![]() .
.
The prior two results show that ![]() . We can also derive some explicit values for linear polynomials (i.e. hyperplane decision boundaries).
. We can also derive some explicit values for linear polynomials (i.e. hyperplane decision boundaries).
Theorem 4. ![]()
Proof. Take ![]() points from
points from ![]() as the vertices of a simplex as follows:
as the vertices of a simplex as follows:
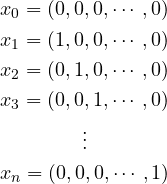
We claim that these points can be correctly classified for any label assignment. Let ![]() denote the indices of the points that are assigned a + label. We construct a linear polynomial
denote the indices of the points that are assigned a + label. We construct a linear polynomial ![]() such that
such that
![Rendered by QuickLaTeX.com \[p(x_i) = \begin{cases}1 &\text{if } i \in I \\0 &\text{if } i \notin I \\\end{cases}\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-59078bb7aaec843918375fab87f57077_l3.png)
giving us exactly the desired classification. There are two cases:
- If
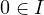 , then we take
, then we take ![Rendered by QuickLaTeX.com p(x) = 1 - \sum_{j \notin I} x[j]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-a220f4c321f364a3fee05cce7c3473d5_l3.png)
- If
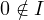 , then we take
, then we take ![Rendered by QuickLaTeX.com p(x) = \sum_{i \in I} x[i]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-7096c3fc61dbecdf5a11a3c7e0c77eb7_l3.png)
It is easy to see that ![]() gives the correct activation in both cases. Thus, we have shown that there exists a set of
gives the correct activation in both cases. Thus, we have shown that there exists a set of ![]() points that can always be shattered.
points that can always be shattered.
We now present the main result, an asymptotic lower bound for arbitrary dimension and degree. We begin with the special case of ![]() and then show that the approach generalizes.
and then show that the approach generalizes.
Theorem 5. ![]()
Proof. Consider a set of ![]() points in the plane arranged as the vertices of an
points in the plane arranged as the vertices of an ![]() integer lattice (with
integer lattice (with ![]() to be determined later). In particular, take
to be determined later). In particular, take ![]() . Assign +1/-1 values to the points arbitrarily. Now, consider each row of the lattice independently, and fit a 1D interpolating polynomial
. Assign +1/-1 values to the points arbitrarily. Now, consider each row of the lattice independently, and fit a 1D interpolating polynomial ![]() to row
to row ![]() . We wish to construct a 2D polynomial out of the
. We wish to construct a 2D polynomial out of the ![]() ‘s by somehow interpolating between them. To do this, define the following family of “selector” polynomials. Let
‘s by somehow interpolating between them. To do this, define the following family of “selector” polynomials. Let ![]() be the 1D polynomial that interpolates:
be the 1D polynomial that interpolates:
![]()
Informally, ![]() “selects” point
“selects” point ![]() while rejecting all others. We can now define our 2D polynomial as follows.
while rejecting all others. We can now define our 2D polynomial as follows.
![Rendered by QuickLaTeX.com \[p(x, y) = \sum_{i=0}^{N-1} p_i(x) \cdot \phi_i(y)\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-e6f055ab4d89f44b4be4943fb8f68d6a_l3.png)
We can see that ![]() selects the appropriate row and
selects the appropriate row and ![]() gets the appropriate value from that row, thus correctly interpolating the full dataset. Since
gets the appropriate value from that row, thus correctly interpolating the full dataset. Since ![]() and
and ![]() are both of degree
are both of degree ![]() , the resulting
, the resulting ![]() is of degree
is of degree ![]() . We require this quantity to be less than
. We require this quantity to be less than ![]() , so we take
, so we take ![]() . We have thus demonstrated a way to correctly classify
. We have thus demonstrated a way to correctly classify ![]() 2D points using a 2D polynomial of degree
2D points using a 2D polynomial of degree ![]() regardless of labelling. Therefore,
regardless of labelling. Therefore, ![]() .
.
Theorem 6. ![]()
Proof. The proof of Theorem 5 generalizes nicely. We will construct an arrangement of points in ![]() that can be shattered. First, consider the largest arrangement of points in
that can be shattered. First, consider the largest arrangement of points in ![]() that can be shattered by a polynomial of degree
that can be shattered by a polynomial of degree ![]() ; that is, an arrangement of
; that is, an arrangement of ![]() many points. Take
many points. Take ![]() copies of this arrangement and stack them along the
copies of this arrangement and stack them along the ![]() th dimension (in 3D, this looks like slices stacked vertically). Assign +1/-1 values to the points arbitrarily. For each slice
th dimension (in 3D, this looks like slices stacked vertically). Assign +1/-1 values to the points arbitrarily. For each slice ![]() , take
, take ![]() as the
as the ![]() -D polynomial that correctly classifies the points. We now define our full
-D polynomial that correctly classifies the points. We now define our full ![]() -D polynomial:
-D polynomial:
![Rendered by QuickLaTeX.com \[p(x) = \sum_{i=0}^{N-1} p_i(x[0], x[1], \cdots, x[n-2]) \cdot \phi_i(x[n-1])\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-959c64c023f4c7eb38c5a05954cd3ca8_l3.png)
We can see that ![]() selects the appropriate slice and
selects the appropriate slice and ![]() gets the appropriate value from that slice, thus correctly interpolating the full dataset. Since
gets the appropriate value from that slice, thus correctly interpolating the full dataset. Since ![]() and
and ![]() are both of degree
are both of degree ![]() , the resulting
, the resulting ![]() is of degree
is of degree ![]() . We require this quantity to be less than
. We require this quantity to be less than ![]() , so we take
, so we take ![]() . We have thus demonstrated a way to correctly classify
. We have thus demonstrated a way to correctly classify ![]() many
many ![]() -D points using a
-D points using a ![]() -D polynomial of degree
-D polynomial of degree ![]() regardless of labelling. Therefore,
regardless of labelling. Therefore,
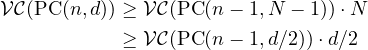
We can solve this recurrence with the base case established by Theorem 5 to obtain the main result:
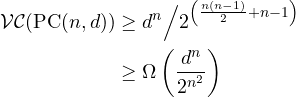
It is exciting to see that the expressive power of polynomial classifiers exhibits (at least) exponential asymptotic growth. However, the curse of dimensionality is strong, with the doubly exponential constant term dependent on ![]() .
.
The results are summarized in the following table

Training GPCs
One immediate way to train a multivariate polynomial classifier is to treat the higher-order terms as the output of a lifting kernel and solve the resulting linear system:
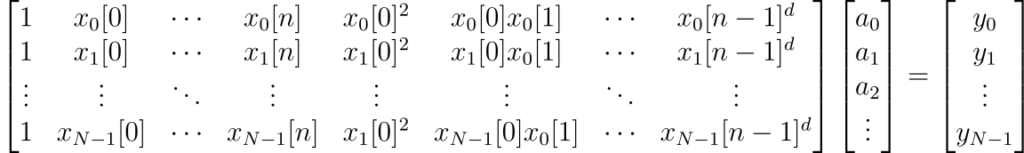
This matrix is a the multivariate analog of the Vandermonde matrix for ordinary polynomial interpolation and is of size ![]() . Solving this system (in the least-squares sense) via SVD requires at least
. Solving this system (in the least-squares sense) via SVD requires at least ![]() operations. If the number of parameters is fixed for a given classifier to-be-trained, this approach is effectively quadratic in the number of training points.
operations. If the number of parameters is fixed for a given classifier to-be-trained, this approach is effectively quadratic in the number of training points.
Another approach is to learn the weights gradually via gradient descent. We can pass the output of the polynomial through a sigmoid function ![]() and then define a cross-entropy loss function. However, this approach may incentivize learning large coefficients so some regulatory terms may be needed in the loss function, or possibly some other kind of non-linear transform on top of the polynomial may be required. Implementing this approach is an avenue for future work.
and then define a cross-entropy loss function. However, this approach may incentivize learning large coefficients so some regulatory terms may be needed in the loss function, or possibly some other kind of non-linear transform on top of the polynomial may be required. Implementing this approach is an avenue for future work.
Conclusion
In this post we investigated the VC-Dimension of the family of generalized polynomial classifiers for binary classification over multi-dimensional feature space. Exact values are computed for low dimension and low degree, and asymptotic bounds are derived for the general form. The quadratic dependence on dimension indicates that the approach may only be suitable for lower-dimension feature spaces in which the degree of the polynomial is much higher than the number of features. However, in these settings, they may prove comparable to neural networks as a universal function approximator.
Methods for training GPC’s were briefly discussed, but more work is required to see if they are really very practical to use (my guess is probably not 😛). Cheers!