A Curious Bound on the Complexity of Graphs With No 4-Cycles
I encountered this rather bizarre looking fact in my undergraduate graph theory class:
Let ![]() be a connected graph with
be a connected graph with ![]() vertices and
vertices and ![]() edges. If
edges. If ![]() does not contain a
does not contain a ![]() -cycle, then
-cycle, then ![]() .
.
This struck me as odd. For an unrestricted graph, the number of edges can be as large as ![]() (e.g. the complete graph). This fact implies that the complexity drops to
(e.g. the complete graph). This fact implies that the complexity drops to ![]() if we simply stipulate that there are no cycles of length
if we simply stipulate that there are no cycles of length ![]() .
.
Let’s dive into a proof. We begin by defining some special subsets of ![]() :
:
![]()
Where ![]() represents the distance (i.e. length of shortest path) from
represents the distance (i.e. length of shortest path) from ![]() to
to ![]() . For example,
. For example, ![]() gives all pairs of adjacent vertices and
gives all pairs of adjacent vertices and ![]() gives all pairs of (non-adjacent) vertices that have a mutual friend. Since the
gives all pairs of (non-adjacent) vertices that have a mutual friend. Since the ![]() ‘s partition the set of all pairs of vertices, we have
‘s partition the set of all pairs of vertices, we have
![Rendered by QuickLaTeX.com \[\binom{n}{2} = \sum_{k \in \mathbb{N}} |D_k|\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-156a6bddd662a3827c5be76ee48cc327_l3.png)
Now, let ![]() and consider the quantity
and consider the quantity ![]() , which counts the pairs of vertices in the neighborhood of
, which counts the pairs of vertices in the neighborhood of ![]() . Either the vertices in these pairs are of distance 1 (if they are adjacent) or they are of distance 2 (since they are both adjacent to
. Either the vertices in these pairs are of distance 1 (if they are adjacent) or they are of distance 2 (since they are both adjacent to ![]() ). Observe that they cannot both be in the neighborhood of any other vertex – otherwise this would form a 4-cycle. Thus, summing over
). Observe that they cannot both be in the neighborhood of any other vertex – otherwise this would form a 4-cycle. Thus, summing over ![]() we count each pair of vertices exactly once:
we count each pair of vertices exactly once:
![Rendered by QuickLaTeX.com \[\sum_{v \in V} \binom{\deg v}{2} = |D_1| + |D_2|\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-9214908012b5180c7927b4c3a048ee8a_l3.png)
We now have:
(1) 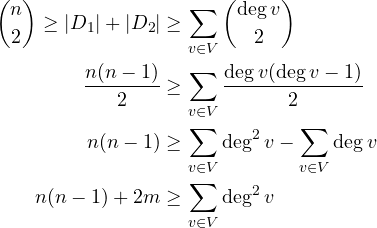
Here we made use of the so-called handshake lemma, which states ![]() .
.
Applying the Cauchy-Schwarz inequality:
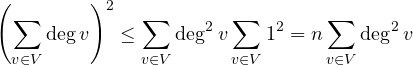
combining with (1):
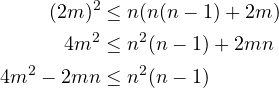
we get a quadratic in ![]() which we solve directly to get the desired result:
which we solve directly to get the desired result:
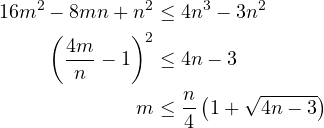
There is a neat construction (due, I think originally, to Erdös) for a family of graphs that achieve this asymptotic upper bound, showing that it is in fact a tight bound. For any prime number ![]() , we construct a graph of order
, we construct a graph of order ![]() by taking our vertices to be
by taking our vertices to be
![]()
Here, ![]() is the finite field of order
is the finite field of order ![]() . Our edge relation is given by
. Our edge relation is given by
![]()
Recall that all arithmetic in this field is done ![]() . It is easy to see that every vertex in the resulting graph will have degree
. It is easy to see that every vertex in the resulting graph will have degree ![]() . Thus,
. Thus, ![]() . We do not necessarily have equality here since there may be self-adjacent vertices. If we decide to exclude these loops for the sake of the construction, the asymptotic complexity does not change.
. We do not necessarily have equality here since there may be self-adjacent vertices. If we decide to exclude these loops for the sake of the construction, the asymptotic complexity does not change.
It remains to show that we have not created any 4-cycles. Indeed, for any two vertices ![]() and
and ![]() , their neighborhoods have at most 1 vertex in common. This follows from the fact that the system
, their neighborhoods have at most 1 vertex in common. This follows from the fact that the system
![Rendered by QuickLaTeX.com \[\begin{cases} ax = b + y \\ cx = d + y \end{cases}\]](https://russ-stuff.com/wp-content/ql-cache/quicklatex.com-aef924fbca9e06591d910f81af63d479_l3.png)
has a unique solution ![]() when
when ![]() and no solution otherwise.
and no solution otherwise.
For example, when ![]() the above construction yields the following graph:
the above construction yields the following graph:

loops omitted: (0, 0), (1, 2), (2, 2)